Vettore nullo

In algebra lineare, il vettore nullo (o elemento zero) di uno spazio vettoriale è l'elemento neutro dell'operazione di addizione definita nello spazio, cioè quel vettore che lascia invariato qualunque vettore dello spazio a cui venga sommato. Tale vettore esiste sempre (per assioma) in qualunque spazio vettoriale, ed è possibile dimostrare che è anche unico.

Definizione

Sia ${\displaystyle V}$ uno spazio vettoriale definito sul campo ${\displaystyle {\mathcal {K}}}$. Dagli assiomi che definiscono lo spazio, esiste un elemento ${\displaystyle \mathbf {0} \in V}$ tale che, se ${\displaystyle :V\times V\to V}$ rappresenta l'operazione di somma tra vettori, allora:

${\displaystyle \mathbf {v} \mathbf {0} =\mathbf {v} \quad \quad {\mbox{ per ogni }}\mathbf {v} \in V}$

Questo è il vettore nullo. Tramite il vettore nullo si definisce (e si dimostra che è unico) l'opposto di un qualunque vettore ${\displaystyle \mathbf {v} \in V}$; esso è il vettore ${\displaystyle -\mathbf {v} }$ tale che:

${\displaystyle \mathbf {v} (-\mathbf {v} )=\mathbf {0} }$.

(si richiede per assioma che ${\displaystyle \mathbf {v} \in V\Rightarrow -\mathbf {v} \in V}$).

Da questi due assiomi segue che il vettore nullo è opposto di se stesso, in quanto per definizione

${\displaystyle \mathbf {0} \mathbf {0} =\mathbf {0} \quad {\mbox{ da cui }}-\mathbf {0} =\mathbf {0} }$.

Unicità

Il vettore nullo è univocamente determinato dalla propria definizione.

Siano infatti ${\displaystyle \mathbf {n} ,\mathbf {n} ^{\prime }}$ due vettori per cui valga la definizione di vettore nullo. Allora

${\displaystyle \mathbf {n} ^{\prime }=\mathbf {n} ^{\prime } \mathbf {n} =\mathbf {n} }$.

Proprietà

Proprietà generali

Si indichi con ${\displaystyle 0}$ l'elemento neutro della somma di ${\displaystyle {\mathcal {K}}}$; il vettore nullo gode delle seguenti proprietà:

• ${\displaystyle 0\mathbf {v} =\mathbf {0} \ \forall \mathbf {v} \in V}$.

Per le proprietà di campo di cui gode ${\displaystyle {\mathcal {K}}}$, 0 ammette opposto e questo è 0, sicché ${\displaystyle 0 0=0}$:

${\displaystyle 0\mathbf {v} =(0 0)\mathbf {v} =0\mathbf {v} 0\mathbf {v} }$

(distributività del prodotto per uno scalare). Per gli assiomi di spazio vettoriale, esiste l'opposto di ${\displaystyle 0\mathbf {v} }$:

${\displaystyle -0\mathbf {v} 0\mathbf {v} =-0\mathbf {v} (0\mathbf {v} 0\mathbf {v} )}$

Il primo membro è il vettore nullo, per definizione, mentre al secondo membro si applica l'associatività della somma, ottenendo:

${\displaystyle \mathbf {0} =\mathbf {0} 0\mathbf {v} =0\mathbf {v} }$.

• ${\displaystyle \lambda \mathbf {0} =\mathbf {0} \ \forall \lambda \in {\mathcal {K}}}$

L'opposto del vettore nullo è il vettore nullo, sicché ${\displaystyle \mathbf {0} \mathbf {0} =\mathbf {0} }$:

${\displaystyle \lambda \mathbf {0} =\lambda (\mathbf {0} \mathbf {0} )=\lambda \mathbf {0} \lambda \mathbf {0} }$

(distributività del prodotto per uno scalare). Per gli assiomi di spazio vettoriale, esiste l'opposto di ${\displaystyle \lambda \mathbf {0} }$:

${\displaystyle -\lambda \mathbf {0} \lambda \mathbf {0} =-\lambda \mathbf {0} (\lambda \mathbf {0} \lambda \mathbf {0} )}$

Il primo membro è il vettore nullo, per definizione, mentre al secondo membro si applica l'associatività della somma, ottenendo:

${\displaystyle \mathbf {0} =\mathbf {0} \lambda \mathbf {0} =\lambda \mathbf {0} }$.

• ${\displaystyle \lambda \mathbf {v} =\mathbf {0} \Leftrightarrow \lambda =0\vee \mathbf {v} =\mathbf {0} }$

L'implicazione a sinistra ${\displaystyle \Leftarrow }$ segue dalle prime due proprietà. Per quanto riguarda l'implicazione a destra, si supponga che:

${\displaystyle \lambda \mathbf {v} =\mathbf {0} }$

Allora, o ${\displaystyle \lambda =0}$, nel qual caso non c'è nulla da dimostrare, o ${\displaystyle \lambda \neq 0}$, nel qual caso esso ammette inverso per le proprietà di ${\displaystyle {\mathcal {K}}}$, cioè esiste ${\displaystyle \lambda ^{-1}}$ tale che ${\displaystyle \lambda ^{-1}\lambda =1}$, dove 1 è l'elemento neutro della moltiplicazione in ${\displaystyle {\mathcal {K}}}$. Per gli assiomi di spazio vettoriale, ${\displaystyle 1\mathbf {v} =\mathbf {v} }$ sicché:

${\displaystyle \lambda ^{-1}\lambda \mathbf {v} =\lambda ^{-1}\mathbf {0} }$

${\displaystyle \mathbf {v} =\mathbf {0} }$.

• Un insieme di vettori che includa il vettore nullo è necessariamente linearmente dipendente; questo vale anche qualora l'insieme consti del solo vettore nullo. Data infatti una combinazione lineare di un simile sistema di vettori, è sufficiente porre tutti i coefficienti uguali a zero tranne quello che moltiplica il vettore nullo, e il risultato sarà zero.

• Per ogni base fissata ${\displaystyle \{\mathbf {e} _{1},\ldots ,\mathbf {e} _{n}\}}$ dello spazio finito-dimensionale ${\displaystyle V}$, il vettore delle coordinate del vettore nullo è il vettore ${\displaystyle (0,0,\cdots ,0)^{T}}$.

Valga la scrittura in coordinate

${\displaystyle \mathbf {0} =c_{1}\mathbf {e} _{1} \ldots c_{n}\mathbf {e} _{n}}$

Allora, poiché ${\displaystyle \mathbf {0} \mathbf {0} =\mathbf {0} }$:

${\displaystyle \mathbf {0} \mathbf {0} =(c_{1} c_{1})\mathbf {e} _{1} \ldots (c_{n} c_{n})\mathbf {e} _{n}=c_{1}\mathbf {e} _{1} \ldots c_{n}\mathbf {e} _{n}}$

da cui, essendo i vettori di base linearmente indipendenti:

${\displaystyle {\begin{cases}c_{1} c_{1}=c_{1}\\\vdots \\c_{n} c_{n}=c_{n}\end{cases}}}$

per cui ${\displaystyle c_{1}=\ldots =c_{n}=0}$.

• Il vettore nullo deve necessariamente appartenere a qualunque sottoinsieme non vuoto di uno spazio vettoriale in cui sia garantita l'esistenza dell'opposto e la chiusura rispetto a combinazioni lineari (un tale sottoinsieme è detto sottospazio vettoriale, e si dimostra essere a sua volta uno spazio vettoriale). In particolare, l'insieme costituito dal solo vettore nullo è uno spazio vettoriale (nonché lo spazio vettoriale di minima cardinalità possibile): esso è un sottospazio di qualunque spazio vettoriale, e la sua dimensione è per definizione 0.

Proprietà in spazi più strutturati

• Se in ${\displaystyle V}$ è definito un prodotto scalare o hermitiano non degenere ${\displaystyle (\cdot |\cdot ):V\times V\to {\mathcal {K}}}$, allora

${\displaystyle (\mathbf {v} |\mathbf {x} )=0\;\;\forall \mathbf {x} \in V\quad \iff \quad \mathbf {v} =\mathbf {0} }$.

Questo segue dall'isomorfismo tra un qualunque spazio vettoriale e il suo spazio duale (l'insieme dei funzionali lineari definiti su di esso). In questo senso, al vettore nullo corrisponde tramite isomorfismo il funzionale nullo.

• Se ${\displaystyle (V,\|\cdot \|)}$ è uno spazio normato, allora per definizione

${\displaystyle \|\mathbf {v} \|=0\quad \iff \quad \mathbf {v} =\mathbf {0} }$;

(questo non vale negli spazi seminormati).

• Negli spazi tridimensionali su cui è definito il prodotto vettoriale il vettore nullo ha la proprietà di annullare sempre il prodotto; inoltre, il prodotto tra due vettori non nulli è il vettore nullo se e solo se questi due vettori sono proporzionali.

Esempi particolari

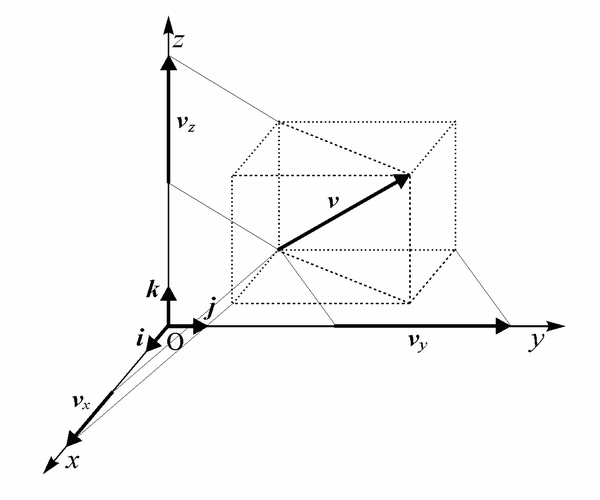
Nello spazio ${\displaystyle \mathbb {R} ^{n}}$ (o ${\displaystyle \mathbb {C} ^{n}}$) il vettore nullo rappresenta l'origine degli assi coordinati.

Negli spazi di funzioni (con somma e moltiplicazione per scalare definiti puntualmente) il vettore nullo è la funzione nulla, cioè la funzione che manda il proprio dominio in ${\displaystyle \{0\}}$.

Nello spazio ${\displaystyle M_{m,n}({\mathcal {K}})}$ delle matrici ${\displaystyle m\times n}$ a coefficienti nel campo ${\displaystyle {\mathcal {K}}}$, il vettore nullo è la matrice i cui elementi sono tutti zero.

Note

Bibliografia

• S. Lang, Algebra lineare, Torino, Bollati Boringhieri, 2009 [1970], ISBN 978-88-339-5035-8..

Voci correlate

• Spazio vettoriale
• Vettore (matematica)

Collegamenti esterni

• (EN) Eric W. Weisstein, Zero Vector, su MathWorld, Wolfram Research.